There is a strong belief among the investor community about the relationship between risk and return.
“Higher the risk, higher the profit.”
It’s valid to a great extent. But let’s try to answer this question, “Was the risk worth it?”
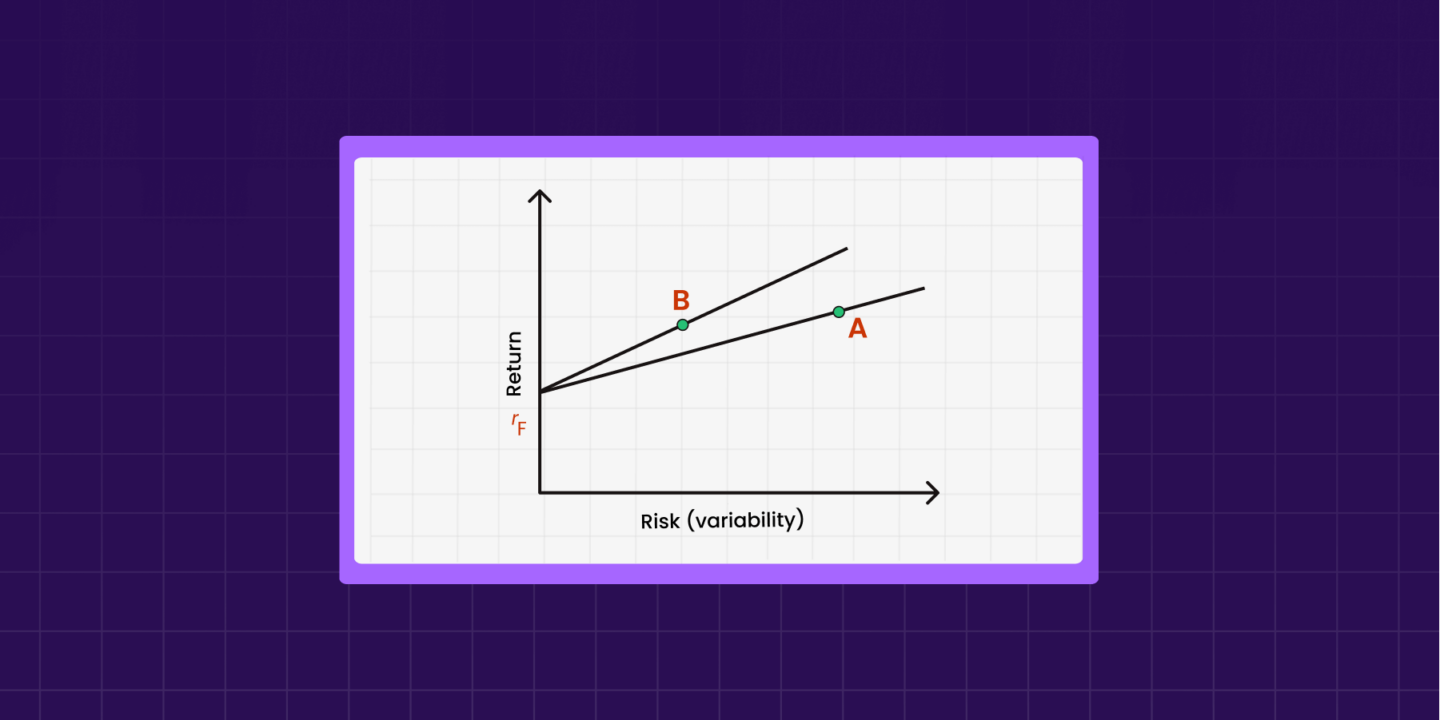
It might be challenging to answer when looking at one single fund or portfolio. Let’s compare two different portfolios, A and B. Both portfolios offer the same return but at varying risk levels. The risk associated with portfolio A is higher than portfolio B.
Unless you want some adrenaline rush, any sensible investor will go for portfolio B as it carries a lower risk for the same return.
Now you might think, how can I compare different funds based on their risk and return level?
We have good news for you. There is a mathematical formula that helps to do just that. It’s called the ‘Sharpe ratio.’ Read on to understand what the Sharpe ratio is, its formula, and its advantages and limitations.
Meaning of Sharpe Ratio
Sharpe ratio is a way to calculate a fund’s risk-adjusted return. It’s a quantitative metric that helps to analyze the investment return in proportion to the risk taken by investing in it.
Sharpe ratio indicates The relative performance of an equity investment compared to the rate of return on a risk-free investment.
American economist William F Sharpe created the ‘Sharpe ratio’ in 1966. Since then, this ratio has been widely adopted among investors. The credibility of this metric skyrocketed when Sharpe won the Nobel Memorial Prize in Economics Science in 1990.
The ratio describes how much the returns improve for every additional unit of volatility the investors face. It helps them understand whether their return is worth the risk. If the Sharpe ratio shows a higher value, the returns are more significant than the risk taken, hence a good investment.
Every investor wants more returns by taking minimal risk. They can play with the Sharpe ratio to analyze the available investment opportunities and find the most optimal one. In fact, it doesn’t take a lot of investing skills.
Sharpe Ratio Formula
The Sharpe Ratio formula goes like this:
Sharpe Ratio = (Rp – Rf) / σp
Where,
Rp = Return of the portfolio
Rf = Risk-free return rate
σp = Standard deviation of the portfolio’s return
1. Return of the portfolio (Rp)
Rp can be the realized historical or expected return of the portfolio.
2. Risk-free return rate (Rf)
The return from Government Securities (G-Sec) is considered for the risk-free return rate (Rf). It’s the safest investment product in the market with almost negligible risk.
3. Standard deviation (σp)
Standard deviation signifies the volatility level of a portfolio by calculating how much the portfolio return differs from its mean value. It considers both the positive and the negative deviation from the average returns. Standard deviation is high for risky asset classes, as the fluctuations can be high in both directions.
The calculation can be performed in three simple steps.
- For calculating the Sharpe ratio of an investment for a time period (let’s say ten years), we should consider the same period for all the parameters (Rp, Rf, and σp).
- Subtract the risk-free return of an asset from the overall portfolio return.
- Divide the resulting number (the excess returns) by the standard deviation of the asset’s returns.
How to calculate Sharpe ratio ?
For example, an investor currently holds a portfolio with an annual return of 18% last year. If the risk-free rate is 6% and the annualized standard deviation is 10%, this gives a one-year Sharpe ratio of 1.2, or (18 – 6) / 10.
Now, the investor is looking to add another asset to the portfolio. It can reduce the standard deviation or volatility to 7%. But it can also lower the portfolio’s overall return to 16% for the coming year. If we calculate the one-year Sharpe ratio for this new portfolio, it comes out to be 1.4, or (16 – 6) / 7.
As you can notice, the Sharpe ratio went up from 1.2 to 1.4 due to the adjustments in the portfolio. Though the return is lesser in the new portfolio, the Sharpe ratio is higher. It indicates the investor limits the potential loss in the new portfolio, thereby reducing the overall risk.
What Is the Importance of the Sharpe Ratio?
For every investor, the risk-reward equation is of paramount importance.
Thus, investors with an existing portfolio can adjust their funds to balance the risk-reward equation based on the Sharpe ratio.
Also, it helps in comparing different portfolios to pick the suitable one based on their risk factor and return potential.
The financial market has multiple asset classes, including shares, bonds, ETFs, deposits, commodities, real estate, and cryptocurrencies. Each security has its own underlying risk-return level that influences the Sharpe ratio.
For example, suppose an investment manager has a portfolio of stocks with a ratio of 1.10. The fund manager adds some commodities to diversify the portfolio, pushing the Sharpe ratio to 1.50 and the return by 20%. It is a good move, considering the increase in the Sharpe ratio.
Let’s consider another scenario. Suppose the portfolio change increases the return by 50% but lowers the ratio to 0.5. The attractive returns might not be worth it as they carry an unacceptable risk level.
Advantages and Disadvantages of Sharpe Ratio
Any metric in the financial world has both pros and cons. Thus, a prudent investor must understand both sides of the story. Let’s start with the good part.
Advantages of sharpe ratio
1. Analyze the fund’s performance
It’s frequently used to assess the performance of mutual funds. It signals the risk level of the fund pertaining to its return potential.
2. Portfolio diversification
By understanding the returns received against the risk taken, the investors or fund managers can adjust their portfolios to balance the risk-reward equation.
3. Comparison tool
It can compare different assets/funds to analyze risk factors and adjusted return rates. Per the benchmark, investors can easily pick the right fund based on their financial goals and risk appetite. For instance, a fund giving 12% returns seems more attractive than a fund offering 10%. But it all changes if the high-return fund has a lower Sharpe ratio than the other fund.
Now, let us look into the limitations of the Sharpe ratio.
Disadvantages
1. Scope for manipulation
Fund managers can manipulate the Sharpe ratio as per their needs. They do this by lengthening the return period, resulting in a lower volatility estimate. Typically, the standard deviation or volatility of annual returns is lower than that of monthly returns. Thus, a 10Y Sharpe ratio won’t be suitable if you want to invest for a three-year time horizon.
2. Highly skewed data points
The standard deviation used in the formula calculates the volatility based on a normal or symmetrical distribution. The normal distribution assumes that the data near the mean value has a high likelihood of occurrence.
But, in reality, the returns in financial markets don’t necessarily follow this pattern. There can be frequent random dips and uptrends influencing the average return value. Thus, the ratio might not tell the entire picture regarding the risk associated with the portfolio.
3. Unsuitable for short-term investments
The ratio is not particularly useful for traders looking for short-term guidance, as it’s designed to analyze long-term investments. Though you can calculate a one-day or one-week Sharpe ratio, it’s not reliable enough to execute short-term trades.
Examples of Good Sharpe Ratio
Sharpe ratio has the following grading thresholds.
- Less than 1: Bad
- 1 to 1.99: Adequate/Good
- 2 to 2.99: Very Good
- 3 and Above: Excellent
Conclusion
Sharpe ratio is one of the most standard methods that helps investors identify the risk level and adjusted return rate before investing in an asset or a fund.
It gained popularity because anyone with basic knowledge can easily calculate and interpret the ratio. If you have learned at least one thing from this article, it would be this — “Higher the Sharpe ratio, the more attractive the return compared to the risk taken.”
FAQs
1. What is a good Sharpe ratio?
Sharpe ratio has the following grading thresholds.
- Less than 1: Bad
- 1 to 1.99: Adequate/Good
- 2 to 2.99: Very Good
- 3 and Above: Excellent
A Sharpe ratio is good if the score is 1 or above.
2. What does a Sharpe ratio of 0.5 mean?
Let’s use the above grading levels to assess the Sharpe ratio.
A Sharpe ratio of 0.5 indicates that the volatility might be much higher for the expected return of the respective fund or portfolio. But it does not provide many insights about the fund’s performance if measured in isolation. Thus, one can use it to compare different funds or asset classes.
3. What is the Morningstar Sharpe ratio?
Sharpe ratio is a way to find a fund’s risk-adjusted return.
The formula of the Sharpe Ratio goes like this:
Sharpe Ratio = (Rp – Rf) / σp
Where,
Rp = Return of the portfolio
Rf = Risk-free return rate
σp = Standard deviation of the portfolio’s return
During calculation, the above formula should use the same timeframe for all parameters (Rp, Rf, and σp). The Morningstar Sharpe ratio is calculated using a ‘three-year’ timeframe.




